4.3. Latent Variable Models#

Latent Variable models is a general term for models which contain latent variables. These are hidden and not observed, but we may either be interested in them or may have to marginalise them out to perform inference. They can be used for expressing complicated densities that cannot be described by an exponential family distribution, or to cluster data points.

The simplest of such models is the Gaussian Mixture Model (GMM), which we will investigate.

4.3.1. Gaussian Mixture Model#

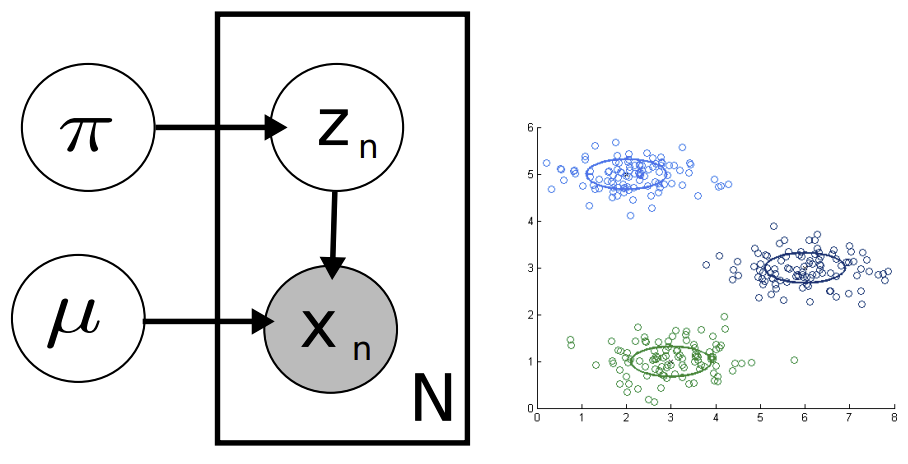
../../_images/GMMs.png

Fig. 4.12 GMM Graphical Representation, Synthetic Data#

In this model, we assume that the data is generated from a mixture of Gaussians, where the latent variable is the identity of the Gaussian from which the data was generated. The model is as follows:

  • \(z_n\) is the multinomial latent variable, which determines the mean \(x_n\) is centered around.

  • \(\pi\) is a parameter for \(z_n\), which is a vector of probabilities for each of the \(K\) Gaussians. \(\pi = (\pi_1, ...\pi_k)\), where \(\pi_i\) is the probability that \(z_n = i\).

  • \(\mu\) is also a vector of length \(K\), where \(\mu_i\) is the mean of the \(i\)th Gaussian.

The joint can be written as follows:

\[ p(x_{1:N}, z_{1:N} | \pi, \mu_{1:K}) = \prod_{n=1}^N p(z_n | \pi) p(x_n | z_n, \mu_{1:K}) \]

In our interest to do ML estimation on the parameters of the model, we need to obtain the marginal probability of the data given the parameters. To do so it is necessary to marginalize out unobserved variables, which in our case are the cluster assignments:

\[ p(x_{1:N} | \pi, \mu_{1:K}) = \prod_{n=1}^N \sum_{z} p(z_n | \pi) p(x_n | z_n, \mu_{1:K}) \]

The log likelihood is then:

(4.7)#\[\begin{align} \log p(x_{1:N} | \pi, \mu_{1:K}) &= \sum_{n=1}^N \log \sum_{z} p(z_n | \pi) p(x_n | z_n, \mu_{1:K}) \\ &= \sum_{n=1}^N \log \biggl[ \sum_{z} \biggl( \prod_{i} \mu_i^{z_n^i} \biggr) \biggl( \prod_{i} p(x_n | \mu_i)^{z_n^i} \biggr) \biggr] \\ \end{align}\]

Because we had to marginalize out latent variables the sum is inside the logarithm, which makes the maximization problem cumbersome.

We could simply use a black-box algorithm for optimization. However, we can exploit characteristics of the log likelihood, and we do so by deriving the EM (expectation-maximization) algorithm.